Kapasitansi

Kapasitansi

Kapasitansi

Loncat ke navigasiLoncat ke pencarian

Pemisahan muatan dalam sebuah kondensator lempeng-sejajar menciptakan medan elektrik internal. Sebuah peruang dielektrik terpolarisasi (oranye) mengurangi medan elektrik serta meningkatkan kapasitansi.

Simbol umum	C
Satuan SI	farad
Satuan lainnya	μF, nF, pF
Dalam satuan dasar SI	F = A2 s4 kg−1 m−2
Dimensi SI	M−1 L−2 T4 I2
Turunan dari besaran lainnya	C = muatan / tegangan

Bagian dari seri artikel mengenai
Elektromagnetisme
Kelistrikan Magnetisme
Elektrostatika
Magnetostatika
Elektrodinamika
Rangkaian listrik Arus listrik Potensial listrik Tegangan listrik Hambatan Hukum Ohm Rangkaian seri Rangkaian paralel Arus searah Arus bolak-balik Arus bermuatan Arus netral Gaya gerak listrik Kapasitansi Induktansi Impedansi Rongga resonan Panduan gelombang
Rumus kovarian
Ilmuwan

Kapasitansi atau kapasitans adalah ukuran jumlah muatan listrik yang disimpan (atau dipisahkan) untuk sebuah potensial listrik yang telah ditentukan. Bentuk paling umum dari peranti penyimpanan muatan adalah sebuah kapasitor dua lempeng/pelat/keping. Jika muatan di lempeng/pelat/keping adalah +Q dan –Q, dan V adalah tegangan listrik antar lempeng/pelat/keping, maka rumus kapasitans adalah:

${\displaystyle C={\frac {Q}{V}}}$

C adalah kapasitansi yang diukur dalam Farad

Q adalah muatan yang diukur dalam coulomb

V adalah voltase yang diukur dalam volt

Unit SI dari kapasitansi adalah farad; 1 farad = 1 coulomb per volt.

Energi

Energi (diukur dalam satuan joule) yang disimpan dalam sebuah kapasitor sama dengan kerja yang telah dilakukan untuk mengisinya dengan muatan listrik. Anggap sebuah kapasitans sebagai C, yang menyimpan muatan +q di sebuah lempeng dan -q di lempeng yang lain. Memindahkan sebuah elemen muatan yang kecil ${\displaystyle \mathrm {d} q}$ dari satu lempeng ke lempeng yang lain bertentangan dengan beda potensial V = q/C memerlukan kerja ${\displaystyle \mathrm {d} W}$:

${\displaystyle \mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q}$

di mana

W adalah kerja yang diukur dalam joule

q adalah muatan yang diukur dalam coulomb

C adalah kapasitans yang diukur dalam farad

Kita bisa mengetahui energi yang tersimpan dalam sebuah kapasitas dengan mengintegralkan persamaan ini. Dimulai dengan sebuah kapasitans tak bermuatan (q=0) dan memindahkan muatan dari satu lempeng ke lempen yang lain sampai lempeng bermuatan +Q dan -Q membutuhkan kerja W:

${\displaystyle W_{bermuatan}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}CV^{2}=W_{disimpan}}$

Dengan mengombinasikan persamaan di atas untuk kapasitansnya sebuah kapasitor pelat rata, kita mendapatkan:

${\displaystyle W_{disimpan}={\frac {1}{2}}CV^{2}={\frac {1}{2}}\epsilon {\frac {A}{d}}V^{2}}$ .

di mana

W adalah energi yang diukur dalam joule

C adalah kapasitans, diukur dalam farad

V adalah voltase yang diukur dalam volt

Kapasitans dan Arus Pergeseran

Fisikawan bernama James Clerk Maxwell menemukan konsep arus pergeseran, ${\displaystyle {\frac {\partial {\vec {D}}}{\partial t}}}$, untuk membuat hukum Ampere konsisten dengan kekekalan muatan dalam kasus di mana muatan terakumulasi, contohnya di dalam sebuah kapasitor. Ia menginterpretasikan hal ini sebagai sebagai gerakan nyatanya muatan, bahkan dalam vakum, di mana Maxwell menduga bahwa gerakan nyatanya muatan berhubungan dengan gerakannya muatan dipol di dalam eter. Meski interpretasi ini telah ditinggalkan, koreksi dari Maxwell terhadap hukum Ampere tetap valid (medan listrik yang berubah menghasilkan medan magnet).

Persamaan Maxwell menggabungkan hukum Ampere dengan konsep arus pergeseran dirumuskan sebagai ${\displaystyle {\vec {\nabla }}\times {\vec {H}}={\vec {J}}+{\frac {\partial {\vec {D}}}{\partial t}}}$. (Dengan mengintegralkan kedua sisi, the integral dari ${\displaystyle {\vec {\nabla }}\times {\vec {H}}}$ bisa diganti dengan integralnya ${\displaystyle {\vec {H}}\cdot \mathrm {d} {\vec {l}}}$ di sekeliling sebuah kontur tertutup, dengan begitu mendemonstrasikan interkoneksi dengan formulasinya Ampere.)

Koefisien potensial

Diskusi di atas hanya berlaku dalam kasus dua lempeng konduksi. Definisi C=Q/V masih berlaku bila hanya satu lempeng yang diberikan muatan listrik, dengan ketentuan bahwa garis-garis medan yang dihasilkan oleh muatan itu berakhir seakan-akan lempeng tadinya berada di pusat ruang lingkup bermuatan sebaliknya pada ketakterhinggaan.

C=Q/V tidak berlaku saat jumlah lempeng yang bermuatan lebih dari dua, atau ketika muatan netto di dua lempeng adalah bukan-nol. Untuk menangani kasus ini, Maxwell memperkenalkan konsep "koefisien potensial". Jika tiga lempeng diberikan muatan ${\displaystyle Q_{1},Q_{2},Q_{3}}$, maka voltasenya lempeng 1 adalah

${\displaystyle V_{1}=p_{11}Q_{1}+p_{12}Q_{2}+p_{13}Q_{3}}$,

dan rumus yang sama juga berlaku bagi voltase lainnya. Maxwell memperlihatkan bahwa koefisien potensial adalah simetris, sehingga ${\displaystyle p_{12}=p_{21}}$, dll.

Dualitas kapasitansi/induktansi

Dalam istilah matematika, kapasitas yang ideal bisa dianggap sebagai kebalikan dari induktansi yang ideal, karena persamaan voltase-arusnya dua fenomena bisa dialihragamkan ke satu sama lain dengan menukarkan istilah voltase dan arus.

Kapasitansi sendiri

Dalam sirkuit listrik atau untai elektris atau rangkaian listrik, istilah kapasitansi biasanya adalah singkatan dari kapasitansi saling (Bahasa Inggris: mutual capacitance) antar dua konduktor yang bersebelahan, seperti dua lempengnya sebuah kapasitor. Terdapat pula istilah kapasitansi-sendiri (Bahasa Inggris: self-capacitance), yang merupakan jumlah muatan listrik yang harus ditambahkan ke sebuah konduktor terisolasi untuk menaikkan potensial listriknya sebanyak 1 volt. Titik rujukan untuk potensial ini adalah sebuah ruang lingkup/kawasan konduksi berongga teoretis, dari radius yang tak terhingga, yang berpusat pada konduktor. Dengan mempergunakan metode ini, kapasitansi-sendiri dari sebuah kawasan konduksinya radius R adalah:

${\displaystyle C=4\pi \epsilon _{0}R\,}$ [1]

Nilai tipikalnya kapasitansi-sendiri adalah:

• untuk "lempeng" puncaknya generator van de Graaf, biasanya sebuah bola 20 cm dalam radius: 20 pF
• planet Bumi: sekitar 710 µF

Elastansi

Kebalikan dari kapasitansi disebut elastansi, dan satuannya adalah reciprocal farad.

Kondensator

Kapasitansi mayoritas kondensator atau kapasitor yang digunakan dalam rangkaian elektronik adalah sejumlah tingkat besaran yang lebih kecil daripada farad. Beberapa sub satuannya kapasitansi yang paling umum digunakan saat ini adalah milifarad (mF), mikrofarad (µF), nanofarad (nF), dan pikofarad (pF).

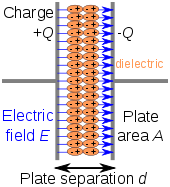
Kapasitansi bisa dikalkulasi dengan mengetahui geometri konduktor dan sifat dielektriknya penyekat di antara konduktor. Sebagai contoh, besar kapasitansi dari sebuah kapasitor “pelat-sejajar” yang tersusun dari dua lempeng sejajarnya seluas A yang dipisahkan oleh jarak d adalah sebagai berikut: is approximately equal to the following:

${\displaystyle C=\epsilon _{r}\epsilon _{0}{\frac {A}{d}}}$ (in SI units)

di mana

C adalah kapasitansi dalam farad, F

A adalah luas setiap lempeng, diukur dalam meter persegi

ε_r adalah konstanta dielektrik (yang juga disebut permitivitas listrik relatif) dari bahan di antara lempeng, (vakum =1)

ε₀ adalah permitivitas vakum atau konstanta listrik di mana ε₀ = 8.854x10^-12 F/m

d adalah jarak antar lempeng, diukur dalam meter

Persamaan di atas sangat baik digunakan jika d besarnya kecil bila dibandingkan dengan dimensi lainnya lempeng. Dalam satuan CGS, persamaannya berbentuk:

${\displaystyle C=\epsilon _{r}{\frac {A}{d}}}$

di mana C dalam kasus ini memiliki satuan panjang.

Tetapan dielektrik bagi sejumlah perubahan dielektrik yang sangat berguna sebagai sebuah fungsi medan listrik terapan, misalnya bahan-bahan feroelektrisitas, sehingga kapasitansi untuk berbagai peranti ini tak lagi sekadar memiliki fungsi alat geometri. Kapasitor yang menyimpan tegangan sinusoidal, tetapan dielektrik, merupakan sebuah fungsi frekuensi. Tetapan dielektrik ubahan berfrekuensi disebut sebagai tebaran dielektrik, dan diatur oleh berbagai proses relaksasi dielektrik, seperti kapasitansi relaksasi Debye.

Buka juga :

• Admitansi
• Kapasitansi
• Ignition Coil - Pengertian, Cara Kerja dan Gambar Konstruksi